(单词翻译:单击)
数学模拟题
1. 145 300 610 1230
In the above sequence every term after the first is formed by multiplying by x and then adding y, where x and y are positive integers. What is the value of x + y?
2. A confectioner has 500 mint, 500 orange and 500 strawberry flavored sweets. He wishes to make packets containing 10 mint, 5 orange and 5 strawberry sweets. What is the maximum number of packets of this type he can make?
3. If S is the sum of 8,6,4,2 and x, what must be the value of x for x to equal 1/5 S ?
4. 25 per cent of 600 is equal to 15 per cent of what number?
5. What is the maximum number of points of intersection of four distinct lines in a plane?
6. If one edge of a 6-inch ruler is to be marked in 1/10 inch units, how many marks will there be on the edge including the 0 and 6 inch marks?
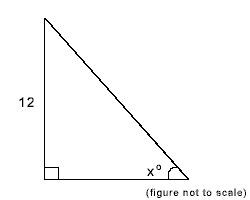
7. If the area of the right triangle above is 72, what is the value of x?
8. Given that the sum of the odd integers from 1 to 99 inclusive is 2500, what is the sum of the even integers from 2 to 100 inclusive?
9. In a certain game of 50 questions, the final score is calculated by subtracting twice the number of wrong answers from the total number of correct answers. If a player attempted all questions and received a final score of 35, how many wrong answers did he give?
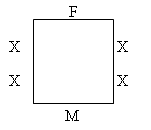
10. Family 1 comprising mother, father and son are to be seated at a table with family 2 comprising mother, father and daughter. The layout of the table is shown in the diagram. F represents one of the fathers and M represents one of the mothers. X represents any family member but with the condition that a male family member must sit opposite a female of the other family. How many different seating plans are possible?
参考答案
参考答案:
1.Correct Answer: 12
Explanation:
Look for a simple relation between the numbers. So if we try multiplying by 2, then 145 becomes 290, to which we need to add 10 to make 300. (If we tried multiplying by 3 the number would be too large. Check with the third term; doubling 300 gives 600 and adding 10 gives 610. So this is the relation, and x = 2 , and y = 10. x + y =12
2.Correct Answer: 50
Explanation:
Since every packet must have 10 mints, this is the limiting factor since the mints will be used up first. 500/10 gives the number of sets of mints = 50 packets can be made.
3.Correct Answer: 5
Explanation:
If x = 1/5 of the sum, then 8 + 6 + 4 + 2 = 4/5 of the sum.
So 20 = 4/5 of S, and 20/4 is 1/5 of S = 5
4.Correct Answer: 1000
Explanation:
Express in math language
(25/100) x 600 = (15/100) n
25 x (600/15) = n
n = 1000
5.Correct Answer: 6
Explanation:
Two lines have one point of intersection. A third line can cut through the other two to give two new points of intersection. (Total = 3). A fourth line can cut through the other three giving three new points of intersection (Total 3 + 3 = 6)
6.Correct Answer: 61
Explanation:
There are sixty tenths to be marked. This will require 61 marks, because you will need a mark for zero. (If you still do not understand, draw out a ruler and count how many marks for two inches, which will be 20 + 1).
7.Correct Answer: 45
Explanation:
Area of a triangle is ½ base x height. ½ x b x 12 =72
Therefore base = 12
This means this is an isosceles right triangle and x =45
8.Correct Answer: 2550
Explanation:
If you write out part of each series like this
1,3,5,7...
2,4,6,8...
You will see that every term in the second series is one more than the corresponding term in the first series. Since there are 50 terms, the second sum will be 50 more than the first = 2500 + 50 = 2550
9.Correct Answer: 5
Explanation:
Let the number of wrong answers = x
Right answers = 50 - x
Subtracting twice wrong from right will give 35
(50 - x) - 2x = 35; 50 - 3x = 35
15 = 3x; 5 = x
10.Correct Answer: 16
Explanation:
Assume Father 1 and Mother 2 are seated as shown. Now select one of the remaining four people for the first vacant seat. We can only choose one of the two people from the other family to sit opposite them (to ensure that the person is of the opposite sex). For the one vacant seat on the same side of the table we have a choice of one out of two, and the final person will have to sit opposite. So with Father 1 and Mother 2 seated first we have a total of 4 x 2 x 2 = 16 arrangements.


