(单词翻译:单击)
第Ⅰ卷(共60分)
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只有一项是满足题目要求的.
1.设集合 M ={x|(x+3)(x-2)<0},N ={x|1≤x≤3},则M∩N =
(A)[1,2) (B)[1,2] (C)( 2,3] (D)[2,3]
【答案】A
【解析】因为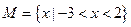 ,所以
,所以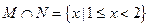 ,故选A.
,故选A.
2.复数z=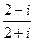 (
(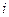 为虚数单位)在复平面内对应的点所在象限为
为虚数单位)在复平面内对应的点所在象限为
(A)第一象限 (B)第二象限 (C )第三象限 (D)第四象限
)第三象限 (D)第四象限
【答案】D
【解析】因为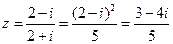 ,故复数z对应点在第四象限,选D.
,故复数z对应点在第四象限,选D.
3.若点(a,9)在函数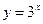 的图象上,则tan=
的图象上,则tan=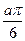 的值为
的值为
(A)0 (B) 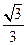 (C) 1 (D)
(C) 1 (D) 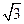
【答案】D
【解析】由题意知:9=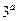 ,解得
,解得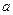 =2,所以
=2,所以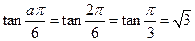 ,故选D.
,故选D.
4.曲线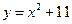 在点P(1,12)处的切线与y轴交点的纵坐标是
在点P(1,12)处的切线与y轴交点的纵坐标是
(A)-9 (B)-3 (C)9 (D)15

5.已知a,b,c∈R,命题“若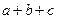 =3,则
=3,则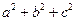 ≥3”,的否命题是
≥3”,的否命题是
(A)若a+b+c≠3,则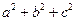 <3
<3
(B)若a+b+c=3,则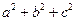 <3
<3
(C)若a+b+c≠3,则
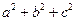 ≥3
≥3
(D)若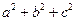 ≥3,则a+b+c=3
≥3,则a+b+c=3
【答案】A
【解析】命题“若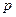 ,则
,则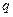 ”的否命题是“若
”的否命题是“若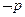 ,则
,则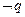 ”,故选A.
”,故选A.
6.若函数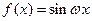 (ω>0)在区间
(ω>0)在区间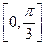 上单调递增,在区间
上单调递增,在区间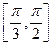 上单调递减,则ω=
上单调递减,则ω=
(A)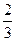 (B)
(B)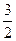 (C
(C )
) 2 (D)3
2 (D)3
【答 案】B
案】B
【解析】由题意知,函数 在
在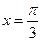 处取得最大值1,所以1=sin
处取得最大值1,所以1=sin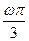 ,故选B.
,故选B.
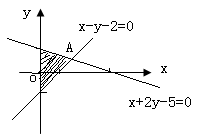 7.设变量x,y满足约束条件
7.设变量x,y满足约束条件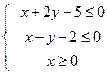 ,则目标函数
,则目标函数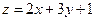 的最大值为
的最大值为
(A)11 (B)10  (C)9 (D)8.5
(C)9 (D)8.5
【答案】B
【解析】画出平面区域表示的可行域如图所示,当直线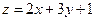 平移至点A(3,1)时, 目标函数
平移至点A(3,1)时, 目标函数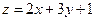 取得最大值为10,故选B.
取得最大值为10,故选B.
8.某产品的广告费用x与销售额y的统计数据如下表

根据上表可得回归方程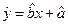 中的
中的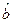 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
(A)63.6万元 (B)65.5万元 (C)67.7万元 (D)72.0万元
【答案】B
【解析】由表可计算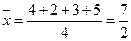 ,
,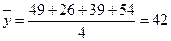 ,因为点
,因为点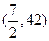 在回归直线
在回归直线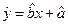 上,且
上,且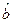 为9.4,所以
为9.4,所以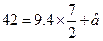 , 解得
, 解得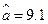 ,故回归方程为
,故回归方程为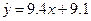 , 令x=6得
, 令x=6得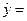 65.5,选B.
65.5,选B.
9.设M(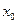 ,
,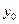 )为
)为 抛物线C:
抛物线C: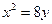 上一点,F为抛物线C的焦点,以F为圆心、
上一点,F为抛物线C的焦点,以F为圆心、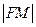 为半径的圆和抛物线C的准线相交,则
为半径的圆和抛物线C的准线相交,则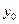 的取值范围是
的取值范围是
(A)(0,2) (B)[0,2] (C)(2,+∞) (D)[2,+∞)
【答案】C
【解析】设圆的半径为r,因为F(0,2)是圆心, 抛物线C的准线方程为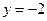 ,由圆与准线相切知4<r,因为点M(
,由圆与准线相切知4<r,因为点M(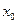 ,
,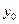 )为
)为 抛物线C:
抛物线C: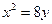 上一点,所以有
上一点,所以有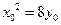 ,又点M(
,又点M(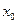 ,
,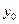 )在圆
)在圆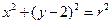 ,所以
,所以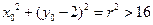 ,所以
,所以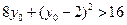 ,即有
,即有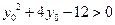 ,解得
,解得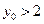 或
或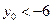 , 又因为
, 又因为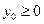 , 所以
, 所以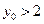 , 选C.
, 选C.
的距离为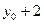 ,
,
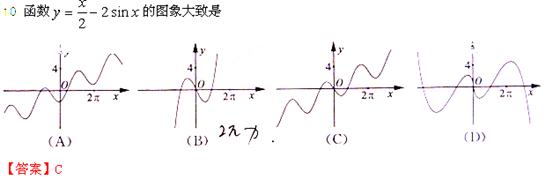
【解析】因为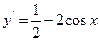 ,所
,所 以令
以令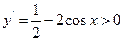 ,得
,得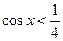 ,此时原函数是增函数;令
,此时原函数是增函数;令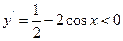 ,得
,得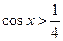 ,此时原函数是减函数,结合余弦函
,此时原函数是减函数,结合余弦函 数图象,可得选C正确.
数图象,可得选C正确.
11.下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱 柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.
柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图. 其中真命题的个数是
其中真命题的个数是
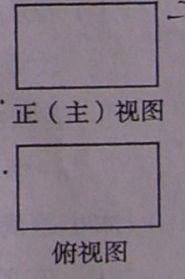
(A)3 (B)2 (C)1 (D)0
【答案】A
【解析】对于①,可以是放倒的三棱柱;容易判断②③可以.
12.设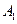 ,
,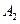 ,
,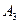 ,
,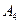 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若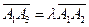 (λ∈R),
(λ∈R),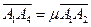 (μ∈R),且
(μ∈R),且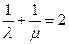 ,则称
,则称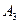 ,
,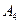 调和分割
调和分割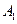 ,
, ,已知点C(c,o),D(d,O)
,已知点C(c,o),D(d,O) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(A)C可能是线段AB的中点
(B)D可能是线段AB的中点
(C)C,D可能同时在线段AB上
(D) C,D不可能同时在线段AB的延长线上
【答案】D
【解析】由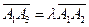 (λ∈R),
(λ∈R),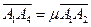 (μ∈R)知:四点
(μ∈R)知:四点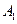 ,
,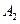 ,
,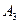 ,
,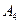 在同一条直线上,
在同一条直线上,
因为C,D调和分割点A,B,所以A,B,C,D四点在同一直线上,且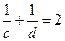 , 故选D.
, 故选D.
第II卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
13.某高校甲、 乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
【答案】16
【解析】由题意知,抽取比例为3:3:8:6,所以应在丙专业抽取的学生人数为40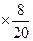 =16.
=16.
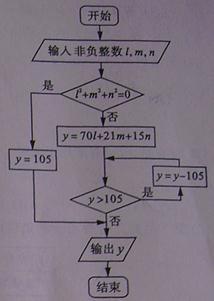
14.执行右图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是 
 【答案】68
【答案】68
【解析】由输入l=2,m=3,n=5,计算得出y=278,第一次得新的y=173;第二次得新的y=68<105,输出y.
15.已知双曲线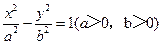 和椭圆
和椭圆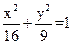 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .

16.已知函数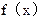 =
=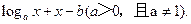 当2<a<3<b<4时,函数
当2<a<3<b<4时,函数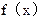
 的零点
的零点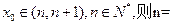 .
.
【答案】5
【解析】方程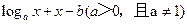 =0的根为
=0的根为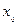 ,即函数
,即函数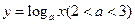 的图象与函数
的图象与函数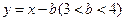 的交点横坐标为
的交点横坐标为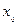 ,且
,且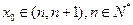 ,结合图象,因为当
,结合图象,因为当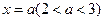 时,
时,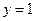 ,此时对应直线上
,此时对应直线上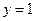 的点的横坐标
的点的横坐标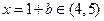 ;当
;当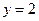 时, 对数函数
时, 对数函数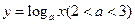 的图象上点的横坐标
的图象上点的横坐标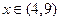 ,直线
,直线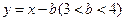 的图象上点的横坐标
的图象上点的横坐标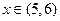 ,故所求的
,故所求的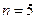 .
.
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
在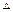 ABC中
ABC中 ,内角A,B,C的对边分别为a,b,c.已知
,内角A,B,C的对边分别为a,b,c.已知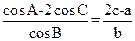 .
.
(I)求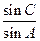 的值;
的值;
(II)若cosB=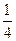 ,
,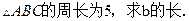
【解析】(1)由正弦定理得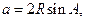
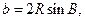
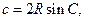 所以
所以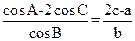 =
=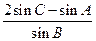 ,即
,即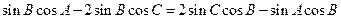 ,即有
,即有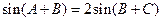 ,即
,即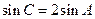 ,所以
,所以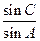 =2.
=2.
(2)由( 1)知
1)知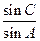 =2,所以有
=2,所以有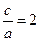 ,即c=2a,又因为
,即c=2a,又因为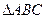 的周长为5,所以b=5-3a,由余弦定理得:
的周长为5,所以b=5-3a,由余弦定理得:
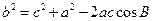 ,即
,即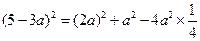 ,解得a=1,所以b=2.
,解得a=1,所以b=2.
18.(本小题满分12分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(I)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(II)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
【解析】(1) 从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男),共9种;选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男 2, 乙男)、(甲女1, 乙女1)、(甲女1, 乙女2),共4种,所以选出的2名教师性别相同的概率为
2, 乙男)、(甲女1, 乙女1)、(甲女1, 乙女2),共4种,所以选出的2名教师性别相同的概率为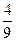 .
.
(2)从报名的6名教师中任选2名,所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男) 、(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2),共15种;选出的2名教师来自同一学校的所有可能的结果为(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2),共6种,所以选出的2名教师来自同一学校的概率为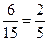 .
.
19.(本小题满分12分)
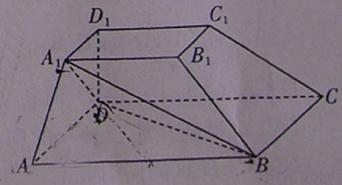
如图,在四棱台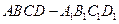 中,
中,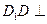 平面
平面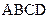 ,底面
,底面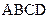 是平行四边形,
是平行四边形,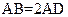 ,
,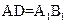 ,
,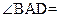 60°
60°
(Ⅰ)证明 :
: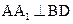 ;
;
(Ⅱ)证明: .
.
【解析】(Ⅰ)证明:因为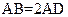 ,所以设
,所以设
AD=a,则AB=2a,又因为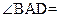 60°,所以在
60°,所以在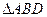 中,由余弦定理得:
中,由余弦定理得: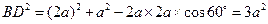 ,所以BD=
,所以BD=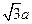 ,所以
,所以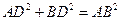 ,故BD⊥AD,又因为
,故BD⊥AD,又因为
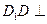 平面
平面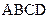 ,所以
,所以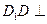 BD,又因为
BD,又因为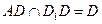 , 所以
, 所以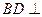 平面
平面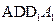 ,故
,故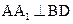 .
.
(2)连结AC,设AC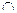 BD=0, 连结
BD=0, 连结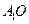 ,由底面
,由底面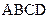 是平行四边形得:O是AC的中点,由四棱台
是平行四边形得:O是AC的中点,由四棱台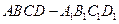 知:平面ABCD∥平面
知:平面ABCD∥平面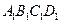 ,因为这两个平面同时都和平面
,因为这两个平面同时都和平面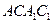 相交,交线分别为AC、
相交,交线分别为AC、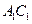 ,故
,故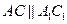 ,又因为AB=2a, BC=a,
,又因为AB=2a, BC=a, 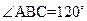 ,所以可由余弦定理计算得AC=
,所以可由余弦定理计算得AC=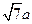 ,又因为A1B1=2a, B1C1=
,又因为A1B1=2a, B1C1=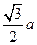 ,
, 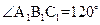 ,所以可由余弦定理计算得A1C1=
,所以可由余弦定理计算得A1C1=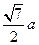 ,所以A1C1∥OC且A1C1=OC,故四边形OCC1A1是平行四边形,所以CC1∥A1O,又CC1
,所以A1C1∥OC且A1C1=OC,故四边形OCC1A1是平行四边形,所以CC1∥A1O,又CC1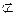 平面A1BD,A1O
平面A1BD,A1O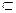 平面A1BD,所以
平面A1BD,所以 .
.
20.(本小题满分12分)
等比数列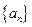 中,
中,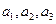 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且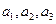 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | 3 | 2 | 10 |
第二行 | 6 | 4 | 14 |
第三行 | 9 | 8 | 18 |
(Ⅰ) 求数列
求数列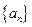 的通项公式;
的通项公式;
(Ⅱ)若数列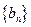 满足:
满足: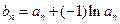 ,求数列
,求数列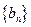 的前
的前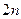 项和
项和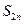 .
.
【解析】(Ⅰ)由题意知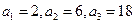 ,因为
,因为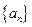 是等比数列,所以公比为3,所以数列
是等比数列,所以公比为3,所以数列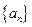 的通项公式
的通项公式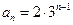 .
.
(Ⅱ)因为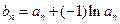 =
=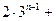
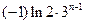 , 所以
, 所以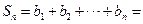
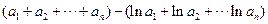 =
=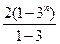 -
-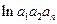 =
=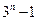 -
-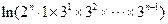 =
=
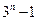 -
-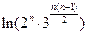 ,所以
,所以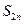 =
=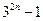 -
-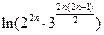 =
=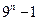 -
-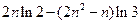 .
.
21.(本小题满分12分)
某 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为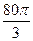 立方米,且
立方米,且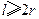 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为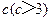 .设该容器的建造费用为
.设该容器的建造费用为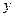 千元.
千元.

(Ⅰ)写出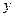
 关于
关于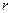 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的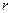 .
.
【解析】(Ⅰ)因为容器的体积为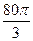 立方米,所以
立方米,所以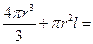
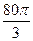 ,解得
,解得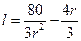 ,所以圆柱的侧面积为
,所以圆柱的侧面积为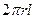 =
=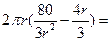
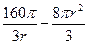 ,两端两个半球的表面积之和为
,两端两个半球的表面积之和为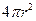 ,所以
,所以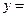
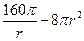 +
+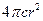 ,定义域为(0,
,定义域为(0,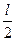 ).
).
(Ⅱ)因为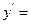
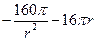 +
+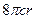 =
=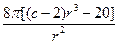 ,所以令
,所以令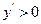 得:
得: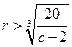 ; 令
; 令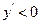 得:
得: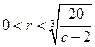 ,所以
,所以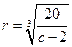 米时,
米时, 该容器的建造费用最小.
该容器的建造费用最小.
22.(本小题满分14分)
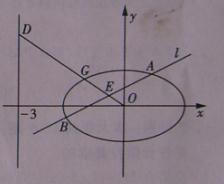
在平面直角坐标系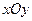 中,已知椭圆
中,已知椭圆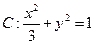 .如图所示,斜率为
.如图所示,斜率为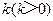 且不过原点的直线
且不过原点的直线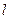 交椭圆
交椭圆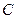 于
于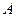 ,
,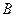 两点,线段
两点,线段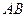 的中点为
的中点为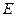 ,射线
,射线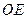 交椭圆
交椭圆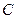 于点
于点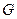 ,交直线
,交直线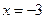 于点
于点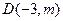 .
.
(Ⅰ)求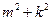 的最小值;
的最小值;
(Ⅱ)若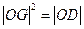 ∙
∙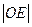 ,(i)求证:直线
,(i)求证:直线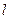 过定点;
过定点;
(ii)试问点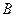 ,
,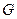 能否关于
能否关于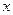 轴对称?若能,求出此时
轴对称?若能,求出此时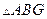 的外接圆方程;若不能,请说明理由.
的外接圆方程;若不能,请说明理由.
【解析】(Ⅰ)由题意:设直线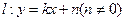 ,
,
由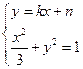 消y得:
消y得: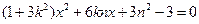 ,设A
,设A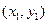 、B
、B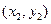 ,AB的中点E
,AB的中点E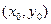 ,则由韦达定理得:
,则由韦达定理得: 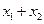 =
=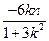 ,即
,即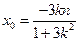 ,
,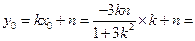
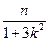 ,所以中点E的坐标为E
,所以中点E的坐标为E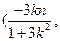
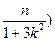 ,因为O、E、D三点在同一直线上,所以
,因为O、E、D三点在同一直线上,所以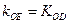 ,即
,即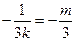 ,解得
,解得
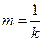 ,所以
,所以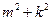 =
=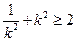 ,当且仅当
,当且仅当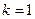 时取等号,即
时取等号,即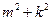 的最小值为2.
的最小值为2.
(Ⅱ)(i)证明:由题意知:n>0,因为直线OD的方程为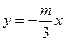 ,所以由
,所以由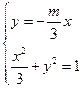 得交点G的纵坐标为
得交点G的纵坐标为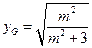 ,又因为
,又因为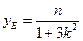 ,
,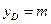 ,且
,且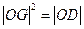 ∙
∙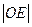 ,所以
,所以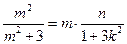 ,又由(Ⅰ)知:
,又由(Ⅰ)知: 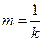 ,所以解得
,所以解得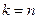 ,所以直线
,所以直线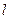 的方程为
的方程为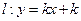 ,即有
,即有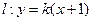 ,令
,令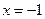 得,y=0,与实数k无关,所以直线
得,y=0,与实数k无关,所以直线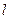 过定点(-1,0).
过定点(-1,0).
(ii)假设点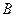 ,
,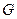 关于
关于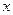 轴对称,则有
轴对称,则有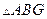 的外接圆的圆心在x轴上,又在线段AB的中垂线上,
的外接圆的圆心在x轴上,又在线段AB的中垂线上,
由(i)知点G(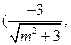
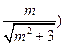 ,所
,所 以点B(
以点B(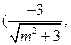
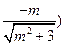 ,又因为直线
,又因为直线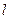 过定点(-1,0),所以直线
过定点(-1,0),所以直线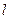 的斜率为
的斜率为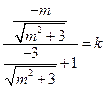 ,又因为
,又因为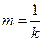 ,所以解得
,所以解得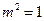 或6,又因为
或6,又因为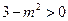 ,所以
,所以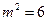 舍去,即
舍去,即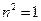 ,此时k=1
,此时k=1 ,m=1,E
,m=1,E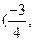
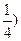 ,AB的中垂线为2x+2y+1=0,圆心坐标为
,AB的中垂线为2x+2y+1=0,圆心坐标为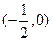 ,G(
,G(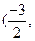
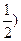 ,圆半径为
,圆半径为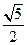 ,圆的方程为
,圆的方程为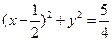 .综上所述, 点
.综上所述, 点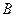 ,
,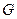 关于
关于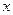 轴对称,此时
轴对称,此时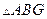 的外接圆的方程为
的外接圆的方程为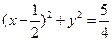 .
.


